Unveiling The Landscape: Diffusion Maps For Data Exploration And Analysis

Unveiling the Landscape: Diffusion Maps for Data Exploration and Analysis

Related Articles: Unveiling the Landscape: Diffusion Maps for Data Exploration and Analysis

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Landscape: Diffusion Maps for Data Exploration and Analysis. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Landscape: Diffusion Maps for Data Exploration and Analysis

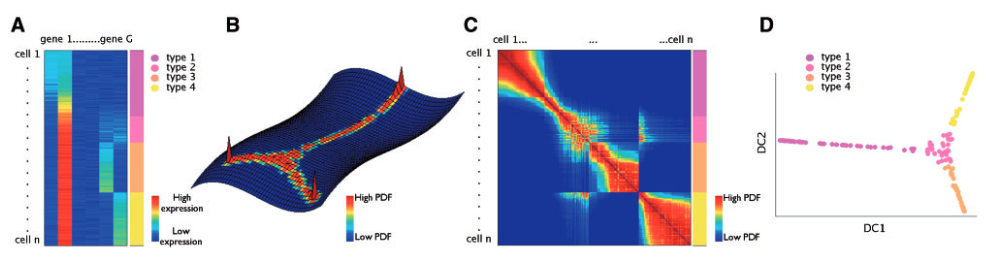
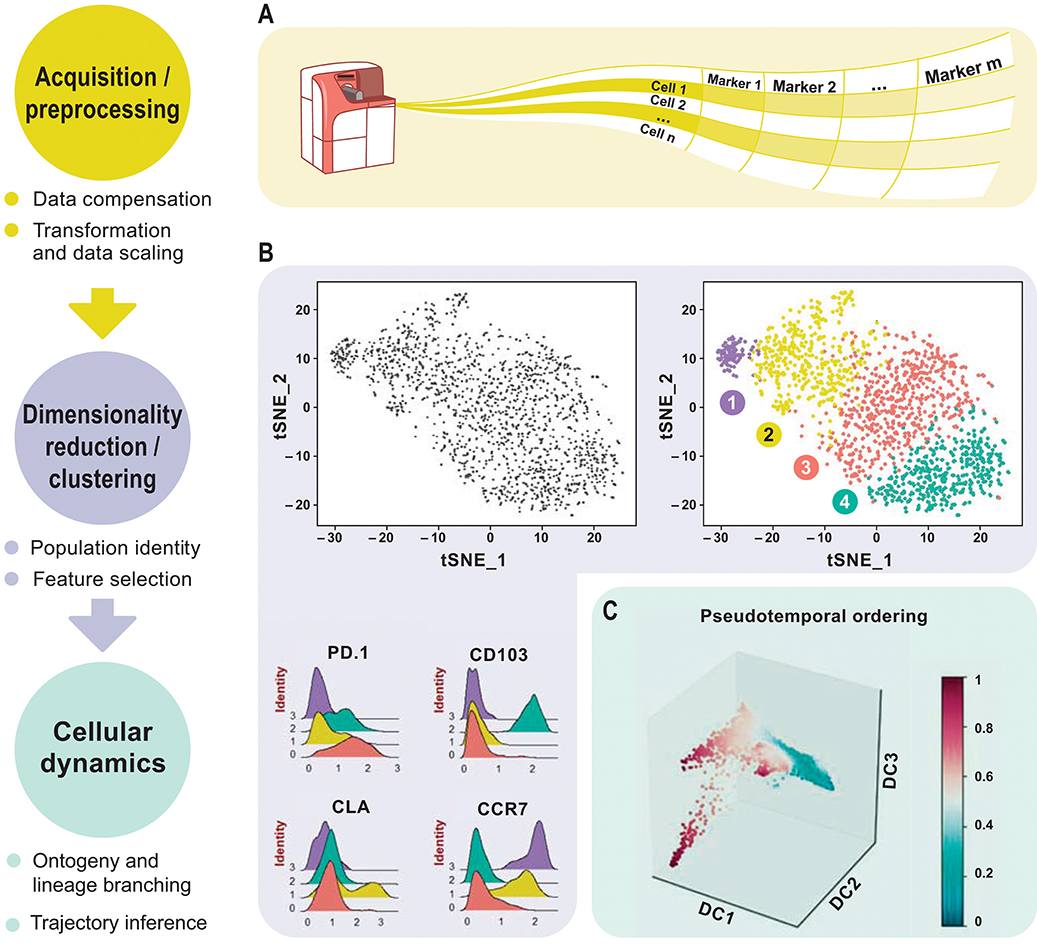
The world of data science is brimming with intricate datasets, each a tapestry woven with complex relationships and hidden patterns. To navigate this labyrinthine landscape, researchers and practitioners require sophisticated tools to extract meaningful insights. Diffusion maps, a powerful technique rooted in the principles of random walks and graph theory, offer a unique perspective for exploring and analyzing high-dimensional data.

Understanding the Essence of Diffusion Maps

Imagine a network of interconnected nodes, each representing a data point. The strength of the connection between two nodes reflects the similarity or proximity between the corresponding data points. Diffusion maps leverage this network structure, employing a probabilistic framework to model the flow of information across the network.

The core concept involves simulating a random walk on the network, where the probability of moving from one node to another is determined by the strength of their connection. As the random walk progresses, the information diffuses across the network, revealing underlying relationships and patterns. Diffusion maps capture this dynamic process by constructing a series of "diffusion coordinates" for each node, effectively embedding the data points into a lower-dimensional space that preserves the essential structure of the original data.

Key Components and Construction

Building a diffusion map involves several crucial steps:

1. Data Representation: The first step is to represent the data as a weighted graph, where each node corresponds to a data point and the weight of the edge connecting two nodes reflects their similarity. This similarity can be measured using various metrics, such as Euclidean distance, cosine similarity, or kernel functions.

2. Diffusion Kernel: The heart of the diffusion map lies in the diffusion kernel, a matrix that encapsulates the probability of transitioning from one data point to another during the random walk. This kernel is typically constructed using a heat kernel, which assigns higher probabilities to transitions between similar data points and lower probabilities to transitions between dissimilar ones.

3. Eigenvalue Decomposition: The diffusion kernel is then subjected to eigenvalue decomposition, yielding a set of eigenvectors and eigenvalues. The eigenvectors, referred to as diffusion coordinates, provide a new representation of the data points in a lower-dimensional space.

4. Dimensionality Reduction: By selecting a subset of the eigenvectors corresponding to the largest eigenvalues, diffusion maps effectively reduce the dimensionality of the data while preserving the most significant information. This allows for visualization and analysis of complex datasets in a more intuitive and interpretable manner.

Benefits and Applications of Diffusion Maps

The power of diffusion maps lies in their ability to:

• Uncover Non-Linear Relationships: Unlike linear dimensionality reduction techniques like Principal Component Analysis (PCA), diffusion maps can capture non-linear relationships and structures hidden within the data.

• Preserve Global Structure: Diffusion maps excel at preserving the global structure of the data, enabling the identification of clusters, manifolds, and other complex geometric patterns.

• Handle Noisy Data: Diffusion maps are robust to noise and outliers, making them suitable for analyzing real-world datasets with imperfections.

• Provide Insights into Data Dynamics: Diffusion maps offer a framework for understanding the dynamics of the data, revealing how information propagates and evolves across the network.

These characteristics make diffusion maps invaluable for a wide range of applications, including:

• Clustering and Classification: Diffusion maps can effectively group data points into clusters based on their intrinsic relationships, facilitating classification tasks.

• Manifold Learning: By uncovering the underlying manifold structure of the data, diffusion maps can provide insights into the geometry and topology of the data space.

• Time Series Analysis: Diffusion maps can be applied to analyze time-dependent data, revealing patterns and trends that evolve over time.

• Image Processing: Diffusion maps find applications in image analysis, particularly in tasks like image segmentation, texture analysis, and object recognition.

• Network Analysis: Diffusion maps can be used to study complex networks, identifying influential nodes and understanding information flow within the network.

FAQs about Diffusion Maps

1. What are the limitations of diffusion maps?

While powerful, diffusion maps do have some limitations:

• Computational Complexity: Constructing a diffusion map can be computationally expensive, especially for large datasets.

• Choice of Parameters: The performance of diffusion maps is sensitive to the choice of parameters, such as the kernel function and the number of eigenvectors used for dimensionality reduction.

• Interpretability: The diffusion coordinates generated by diffusion maps can be difficult to interpret, particularly for high-dimensional datasets.

2. How do diffusion maps compare to other dimensionality reduction techniques?

Diffusion maps offer a distinct advantage over other dimensionality reduction techniques like PCA by capturing non-linear relationships and preserving global structure. However, PCA is generally faster and more computationally efficient.

3. What are some alternative methods for data exploration and analysis?

Other popular methods for data exploration and analysis include:

• t-SNE (t-Distributed Stochastic Neighbor Embedding): A technique that focuses on preserving local neighborhood relationships.

• UMAP (Uniform Manifold Approximation and Projection): A more recent method that aims to preserve both local and global structure.

• Isomap (Isometric Feature Mapping): A method that preserves geodesic distances between data points.

4. How can I learn more about diffusion maps?

Numerous resources are available for learning about diffusion maps:

• Books: "Diffusion Maps and Spectral Clustering" by Ronald Coifman and Stéphane Lafon provides a comprehensive overview of the theory and applications of diffusion maps.

• Articles: Numerous articles on diffusion maps can be found in journals and online repositories such as arXiv.

• Software Packages: Software packages like Python’s scikit-learn and R’s diffusionMap package provide implementations of diffusion maps.

Tips for Using Diffusion Maps

• Data Preprocessing: Ensure that your data is appropriately preprocessed before applying diffusion maps. This may involve normalization, scaling, or outlier removal.

• Parameter Tuning: Experiment with different parameter settings, such as the kernel function, bandwidth, and number of eigenvectors, to optimize the performance of your diffusion map.

• Visualization: Visualize the diffusion coordinates to gain insights into the structure of your data.

• Interpretation: Carefully interpret the results of your diffusion map analysis, considering the context of your data and the specific application.

Conclusion

Diffusion maps offer a powerful framework for exploring and analyzing complex datasets, uncovering hidden relationships and structures that may not be apparent using traditional techniques. By harnessing the principles of random walks and graph theory, diffusion maps provide a unique perspective on data, revealing intricate patterns and facilitating deeper understanding. As data science continues to evolve, diffusion maps remain a valuable tool for navigating the intricate landscape of data and extracting meaningful insights from the ever-growing deluge of information.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Landscape: Diffusion Maps for Data Exploration and Analysis. We appreciate your attention to our article. See you in our next article!